Recent Paper: Boosting the Direct CP Measurement of the Higgs-Top Coupling
/I'm going to describe my most recent paper, written with Dorival Gonçalves, postdoc at the IPPP at Durham University. This is the arXiv version, as is usual in particle physics, we submit to the preprint serve, collect up commentary and citation requests, then get around to submitting to a journal.
In this paper, we're interested in how to both discover the coupling of the Higgs to the top quarks, and then measure the charge-parity (CP) properties of that coupling. The Higgs I've attempted to explain here, and CP I've touched on here. What you need to know for this paper is that the top quark is the most massive quark, and also the most massive Standard Model matter fermion. It has a mass of approximately 175 GeV (with a ~2 GeV error), which about as massive as the nuclei of a element like tungsten. The top was discovered experimentally in 1995 at the Tevatron, though we knew it must exist after 1973 (and indeed you can find some pretty hilarious in hindsight papers over the years which confidently predict the top quark mass). The top quark is actually heavier than the Higgs (with a mass of 125 GeV). We found the top before the Higgs even though the top was heavier because the top is a strongly interacting particle, and so has a larger production cross section as compared to the weakly interacting Higgs. Bigger cross section means more particles produced means easier to find (all else being equal).
As particle physicists, we have a special interest in the top-Higgs interaction (the "coupling"). This is because the top is so massive. Like all Standard Model fermions, the top quark can only have mass in the presence of the Higgs mechanism. Without the Higgs field and its non-trivial vacuum expectation value, the top quark would be two massless fields (the "left-handed" top and "right-handed" top); the Higgs ties those two together into a single massive particle. Now, this is the case for all the quarks and leptons, but the top holds our attention because the large mass of the top implies that it has a very powerful coupling to the Higgs field, much larger than the couplings of any other fermion. The mass of any fermion is proportional to interaction size between the Higgs field and the fermion. This number is called a "Yukawa coupling," and in the Standard Model, the Yukawa for the top quark is close to 1, which is about as big as it can get. Though keep in mind we don't yet know if the Higgs field is really exactly as the Standard Model predicts, so the Yukawa could actually be smaller than 1. The excitation of the Higgs field - the Higgs boson - inherits the couplings of the field, so we predict significant interactions between the top quark and the Higgs itself.
Top quark-induced interaction between Higgs boson and Gluons
Now, part of figuring out if the Higgs we discovered is exactly the Standard Model prediction, or part of some larger and more complicated "Higgs sector" is measuring all of these predicted couplings. Right now, we have measured that the Higgs couples to the force-carriers of the weak force, the $W$ and $Z$ vector bosons, and that those interactions are close to the expected values for "The Higgs Boson." Which is why we say we've discovered "The (or at least A) Higgs Boson." But we haven't measured the couplings to the fermions yet, and those must exist if our understanding of Higgs sector is correct. We've seen indirect evidence of the Higgs-top interaction, since we produce Higgses through an induced "Higgs-gluon" interaction that we suspect is due to a loop of top quarks (see the Feynman diagram here). However, as this is a "loop-induced" interaction, this could be the result some combination of the top-Higgs interaction and something unexpected. We'd like to tease apart the various interactions and see everything clearly and separately.
Keep in mind we'd love to measure these couplings and get the "wrong" answer, since that implies something new is going on. New is good.
So this paper is our contribution of an idea to find the top-Higgs interaction, and measure not only its strength (the size of the Yukawa), but also the CP properties. The Standard Model predicts that the Higgs should be a "CP-even" particle, meaning that the Higgs interactions would be the same for particles and "mirrored" antiparticles (i.e. turn the particles into antimatter and switch the direction that they spin). However, as usual, we want to verify this property. Because if the Higgs acts like a "CP-odd" particle, or some mixture of even-ness and odd-ness, that would incredibly interesting.
Obviously, we're not the first people to think of looking for the Higgs interaction with tops, there is a large body of theoretical and experimental work on this topic. We like to think our addition is helpful for a couple reasons: first, we are the first to do a study of top-Higgs searches using something called the "boosted" Higgs in one particular channel (the "dilepton" mode, as I'll explain shortly). Second, the technique can be extended to not only discover the interaction but measure CP. Third, we do a realistic study including secondard effects, so we're reasonable sure that this theoretical idea will survive contact with reality.
Example diagram for Higgs-Top production at the LHC.
So if you're looking for top-Higgs interactions directly, you'll be interested in events where you produce a pair of top quarks (really a top $t$ and an antitop $\bar{t}$) which then radiate off a Higgs boson. Something like the Feynman diagram I'm showing here.
Now, the top quarks and the Higgs are unstable. They decay, into a myriad of possible final states. Tops decay to $W$ bosons and a bottom quark, and the $W$ decays further into either more quarks or a charged lepton (electron, muon, or tau) and a neutrino. The Higgs can decay into pairs of bottom quarks, or via more $W$ and $Z$ bosons (there are other decay modes, we suspect, but they are very rare). We decided to focus on what's called the "di-leptonic" channel: where both $W$ bosons from top decay decay to leptons, and further require the Higgs to decay to bottom quarks. So our event looks like this: $$ p p \to t\bar{t} H \to (b W^+)(\bar{b} W^-)(b\bar{b}) \to (b \ell^+ \nu)(\bar{b} \ell^- \bar{\nu})(b\bar{b}). $$
This channel has the advantage of being very "clean," as charged leptons are easier to see and disentangle from backgrounds as compared to decays of the $W$ bosons involving quarks. However, since the final state involves neutrinos which are invisible at the LHC, we can't reconstruct the event completely: there will be two "missing" particles which zip through our detector and make it impossible for us to discover the original momenta of the top and antitop quarks. So we have a cleaner event, but we sacrifice some knowledge (we also sacrifice cross section, as these decays are somewhat rare).
Now, we have events with four $b$ quarks, two leptons, and a bunch of missing momentum (from the neutrinos). There are a number of Standard Model non-Higgs events at the LHC which can look just like this signature. So our job is to find ways to preferrentially pick events that are signal and reject events that are background.
This is where our way of looking for CP comes in. Dorival and I were actually looking into a completely different class of physics searches (which I won't tell you about, since we might still write that paper), and stumbled onto a surprising little technique that we could apply to this problem. We noticed that if you measure the "azimuthal angle" between the top and antitop quark, $\Delta\phi_{tt}$, you could get information about the CP properties of the Higgs that is radiated off in these type of events. Moreover, the background had a different distribution in $\Delta\phi_{tt}$ than signal, so not only can you use this variable to measure CP, you can first use it to discover $t\bar{t}H$ production.
Sketch of azimuthal angle, as seen looking down beam axis (direction of proton beam at the LHC).
So what is this azimuthal angle? By "azimuthal" I mean the angle between the direction of the top and antitop if you imagine looking directly down the path of the incoming proton beam. In that case, events radiate out from the center like the hands on a clock, and we just want the angle between the top quark and the antitop. See the figure for a visual.
What we found was that CP-even Higgs bosons (that is, the Higgs as we expect it to be) would tend to be produced in events with the top and anti-top produced "back-to-back," or $\Delta\phi_{tt}$ near $\pi$ radians ($180^\circ$). However, CP-odd Higgses had a slight tendency to be produced with the top and antitop moving in the same direction, $\Delta\phi_{tt} \approx 0$. This first part of our paper is discussing why we expect this behavior to occur. In addition to the explicit calculation we performed in the paper, there's a cute little argument you can make involving taking the mirror image of the event which proves this behavior is expected.
However, this effect is really small. Indeed, if you just take every $t\bar{t}H$ event and look at the distribution, you won't see any noticeable difference. You have to select events where the Higgs is moving "sideways" with a lot of momentum. This is the "boosted" part of our paper. Normally, you'd rather not restrict yourself to this boosted regime, since its relatively rare for Higgses to be produced with a significant sideways "kick," and so requiring one is another big cut in your signal rate. However, we had found this variable, so we decided to run with it. I show here two of the panels of our Figure 1, demonstrating the distribution of $\Delta\phi_{tt}$ both without and with the requirement of a significant boost on the Higgs. The first figure is the distribution without any boost: everything piles up near $\pi$. The second is with a boost. Most things pile up still at $\pi$, but one component of the CP-odd state (which is labeled $0^-$ in the paper) piles up near zero. So if you went and looked at the LHC and saw a bunch of events in this category with $\Delta\phi_{tt} \sim 0$, you'd have some evidence that the Higgs was interacting with the tops like a CP-odd particle, rather than a CP-even.
Now, of course, as I just said I can't measure the direction of the top and antitop, so $\Delta\phi_{tt}$ isn't a physical observable. But it turns out when tops decay, the lepton tends to go in the direction of the top's momentum. Therefore, we can build a proxy variable, $\Delta\phi_{\ell\ell}$, which is the azimuthal angle between the two leptons, and use that to get most of the same information as $\Delta\phi_{tt}$. We explicitly calculated that in our paper, and found again the general behavior that, in the boosted Higgs regime, we got a noticeable difference between CP-even and CP-odd options. I show that here, which is Figure 2 from the paper.
Since we're dealing with the boosted Higgs, we are in a bit of a bind. We're requiring the rarest decay of the tops (dileptonic), and now we need high momentum Higgs. Not looking good. However, we can turn this to our advantage. When a fast moving particle decays, the decay products tend to move in the same direction as their parent. Rather than exploding outward in a sphere, they form a narrower "stream" of particles. When those particle are the two bottom quarks from $H \to b\bar{b}$ decay, we can use a technique called "fat-jet" tagging to look for that particular stream of particles and reject background. This only works if the Higgs is boosted, otherwise there is no stream of energy to look for. Dorival, my coauthor, is an expert in these tagging techniques, so there was a really nice synergy here. To our knowledge, this is the first time anyone has done a serious analysis of the Higgs-top dileptonic final state using boosted Higgs tagging, and Dorival did a huge amount of work to do it right, and control for theoretical uncertainties. So if you're an experimentalist reading this, you can trust the results.
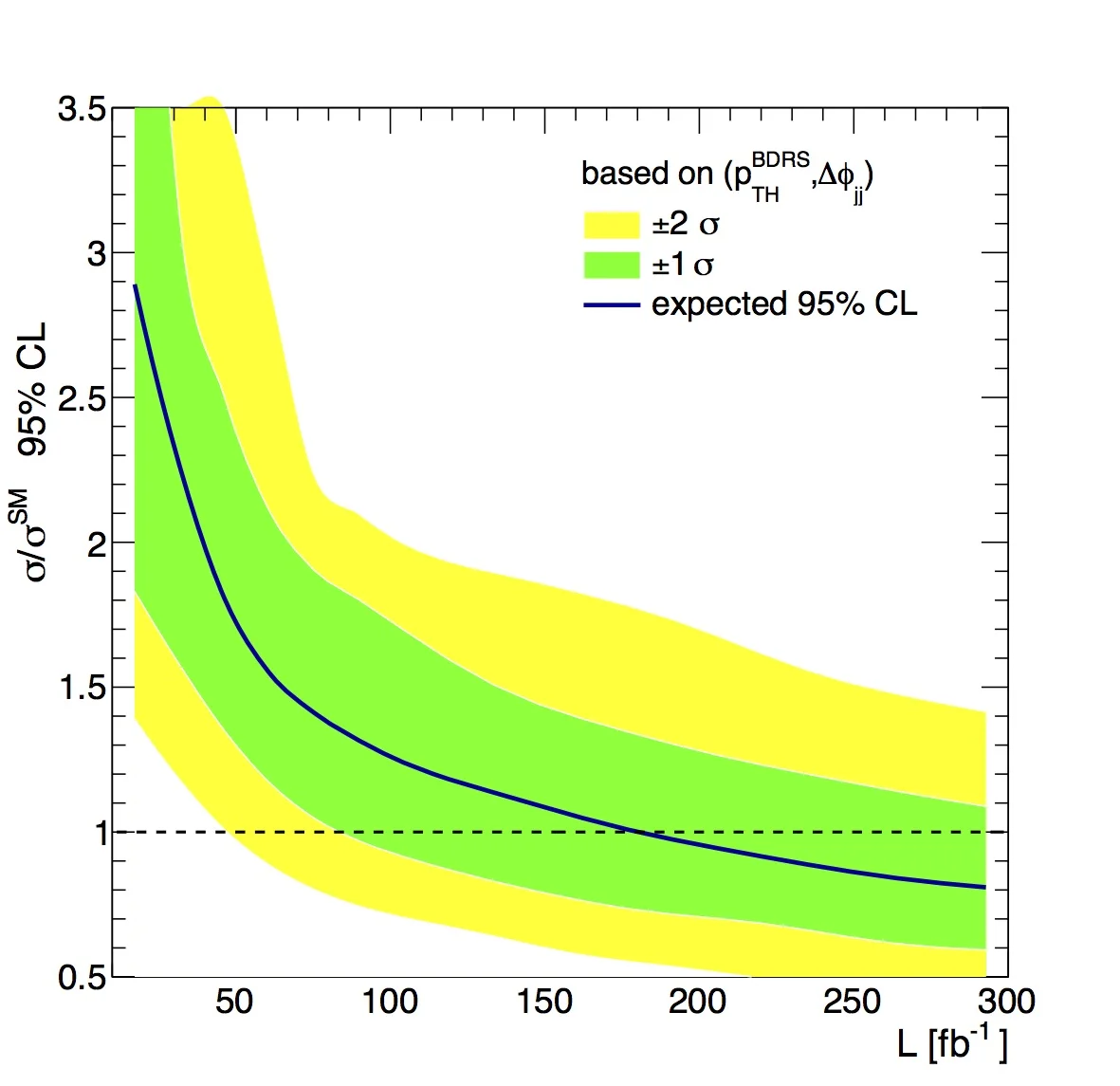
Expected signal strength that can be measured as a function of collected data
One of the results we found was that the backgrounds to our signal had different distributions of $\Delta\phi_{\ell\ell}$ than our signal, for both CP-even and CP-odd Higgses. So the first thing we did is say "using the boosted Higgs tagging, and this new variable (and a few other tricks), how much data do we need to conclusively see the signal of $t\bar{t}H$ production over the backgrounds?" Our Figure 3 (reproduced here), shows how much "luminosity" the LHC would need to discover the Standard Model CP-even Higgs using our technique. You can see we need a few hundred fb$^{-1}$ (see here for an explaination of that unit). This is fairly large amount of data; in the 8 TeV Run-I of the LHC, they collected only 20 fb$^{-1}$. But it's not crazy, it's hopefully a few years of work at Run-II of te LHC.
The green and yellow bands are indications of the uncertainty in our predictions. The black line is what we expect to happen most often. 68% of the time you'll need the amount of data within the green band (the $1\sigma$ line). 95% of the time, you'll fall inside the yellow $2\sigma$ band. This set of colors for the sigma curves has become standard in experimental particle physics, and due to the color scheme, such plots are often called "Brazil plots."
Expected confidence Level at which CP-odd Higgs can be distinguished from CP-even, as a function of collected LHC data.
Finally, how well can we measure CP? Well, we'll need a lot more data. In Figure 5 of the paper (again shown here), we plot the "confidence level" we'd be able to distinguish CP-odd from the CP-even scenario. On average, we'd need an order of magnitude more data than mere discovery. That's many years of LHC running, but it's something we can imagine occuring. And to our knowledge, this is the best-case scenario for this measurement right now. It's hard, but at least we have a path forward. As you can see, though we have discovered "the Higgs," a lot of work remains for us to truly know everything we want to know about it. And who knows, somewhere along the line we might discover one of these difficult precision measurements will give us the "wrong" answer, meaning that our Higgs isn't the simple Standard Model particle. And that will be a lot of fun.
So, this was a technical post, about a paper that is primarily of interest to LHC physicists. But for the lay reader I hope you've at least gotten an idea of the sort of problems we're working on, and the kind of techniques we use. There's lots of work to be done at the LHC, and it may take us many years to accomplish it all. But the Higgs is something new, and we have to study the hell out of it.