Simulating a galaxy without a computer
/The cosmic web of galaxies as seen by SDSS.
A galaxy is a complicated place. Your average spiral galaxy, like the Milky Way, has a few hundred billion stars, each moving in its own complicated orbit. Around the stars and in the space in between, there is gas and dust. In addition to contributing to the gravitational forces in the galaxy, the gas can form clouds that drive star formation. Indeed, the eponymous spiral arms of a spiral galaxy are pressure waves in the gas, causing star formation and a unmistakable pattern of bright young (and thus “blue”) stars that stand out among the older (“red”) stars. As stars go through their lives, the gas around them can be driven by the winds from supernovae, pulling other galactic material around in its gravitational wake.
Finally, there is the dark matter, equal or greater in mass than all the visible material in a galaxy. Without the dark matter, stars in the outer reaches of a spiral galaxy would fly off into intergalactic space, as the gravitational pull of the stars and gas within a galaxy are by themselves insufficient to keep the galaxy together. Dark matter is the glue that binds galaxies.
For particle physicists like myself, understanding how a galaxy works is critical for understanding how dark matter works at the particle level. All our evidence for the properties of dark matter, starting with its very existence and going from there, comes from its gravitational imprint on the visible matter. The physics of the very small influences the structure of some the largest objects in the Universe, and so by studying the latter, we learn about the former.
Cosmic Web of dark matter from the Millennium simulation, tracing the location of matter in the Universe.
But, since a galaxy is so complicated, we can’t determine how they work with pencil and paper. Instead, if we want to know how dark matter plays in to the structure of a galaxy, we have to do it the hard way. You take a bunch of gas and dark matter in a computer simulation and distribute it according to the density perturbations that are suggested by the Cosmic Microwave Background, and then evolve that system forward for a few billion years. When you do that, you get a system that looks remarkably like a spiral galaxy, embedded within a cosmic web of other galaxies.
The comparison with observation is not perfect especially at the smallest scales, which might either an artifact of the computational limitations of our simulations, or maybe it is a sign that there’s something new is going on the dark sector — the particle physics of the dark matter. But just the agreement of galaxy distributions in the Universe agrees so well with simulation tells us that dark matter, whatever it is, was not moving near the speed of light at a particular moment in Cosmic history.
Specifically, it was not moving relativistically at the moment when the energy density of radiation fell to be equivalent to that of non-relativistic matter, which happened when the Universe was a few ten thousand years old and 1/3000th the size it is today, when the seeds of what would become galaxies started growing in the primordial soup. Thus from the distribution and number of galaxies we learn dark matter is “cold” (non-relativistic at that moment in history), not “hot” (moving relativistically), and we can even set precise bounds on how “warm” dark matter was. (As a sidenote, “warm” dark matter is a bit of a sliding scale, which I think gets defined as “whatever level of hotness is not currently ruled out by the data.”)
So as a particle physicist, I’m very interested in the results of N-body simulations of galaxies even though I don’t run them as part of my research, because they directly speak to the problems I’m trying to address.
Which is why I’m going to share the story of an incredibly cool story of the earliest N-body simulation of galaxies. Way back in 1941.
Of course, this simulation by Erik Holmberg only had an $N$ of 74, and wasn’t trying to simulate the entire formation history of a galaxy. Still, what he did was pretty mindblowing.
N-body simulations are called N-body simulations because what you’re doing is trying to evolve forward of system of N particles, interacting through gravity (though today, the best simulations can also include more complicated physics like particle scattering, cooling, star formation, energy injection from supernovae, magnetic fields, etc).
Let’s keep our focus on gravity only, because that’s hard enough. You can exactly solve the motion through time of two gravitationally interacting bodies. Newton did it in the 16th century, and the results are the elliptical orbits which are a good approximation to the orbits of planets in the Solar System.
I say “good approximation” because as soon as you add an extra body (that is, $N=3$), you cannot exactly solve the equations of gravity that predict the motion going forward in time. Famously, the Three-Body Problem has no analytic solution. So, while you can approximate the Earth-Sun system as a two body problem to get our orbit, really you have to add the effects of Jupiter, and Mars, and Venus, and so on and so on
The effects are small, but they can add up, and so if you care about these small effects, you have to approximate the solutions for planetary orbits by brute-forcing the solution. At any moment in time, you take each object, calculate the gravitational force on that object from every other object, and then figure out the change in velocity that acceleration would cause in some timestep. Then, you advance the system forward by that timestep, moving each object with its velocity vector. Now you recalculate, and so on.
The most straightforward brute forcing therefore takes approximately $N^2$ calculations: for each of $N$ objects, you must calculate the force between that one object and $N-1$ other objects, so the whole calculation takes $N(N-1)$ calculations. (For very large $N$, this is basically $N^2$.) There are tricks that can speed up these calculations: you can combine distant objects into one pseudo-object the net force on one object from these distant pseudo-objects. This creates a tree-like structure, and the best codes now can traverse the tree in $\log N$ steps for $N$ objects. Still $N\log N$ is a lot of calculations, especially if you are simulating billions of dark matter and star particles, like the best modern simulations.
The problem quickly becomes intractable unless you can throw immense computing power at it, which just wasn’t possible until very recently. An early computer N-body simulation was the BESK computer in 1961 (see this paper for details). Since then of course, we can do quite a bit better, with modern simulations containing billions of star and dark matter particles.
The trick Holmberg used was to start with the fact that gravity drops off with distance like $1/r^2$ — the force decreases proportional to the distance squared. The reason this happens is very simple (at least in a Newtonian view): it’s just that the gravitational attraction from a mass at a given distance is being “smeared out” over the entire surface area of a sphere. The surface area of a sphere grows as $r^2$, so the force decreases as $1/r^2$.
So the force of gravity drops just due to geometry: we live in a Universe with three spatial dimensions and so spheres have surface areas that go as $r^2$. For exactly the same reason, a lot of other effects in nature drop like $1/r^2$. For example: the intensity of light.
A candle or lightbulb emitting light in a sphere will have the energy it is emitting per second “smeared out” over a larger and larger sphere as the light expands away from the source. Thus, the intensity of light (energy per time per area) must drop like $1/r^2$. (Using this fact is one of the ways we can determine how far away some astronomical objects are.)
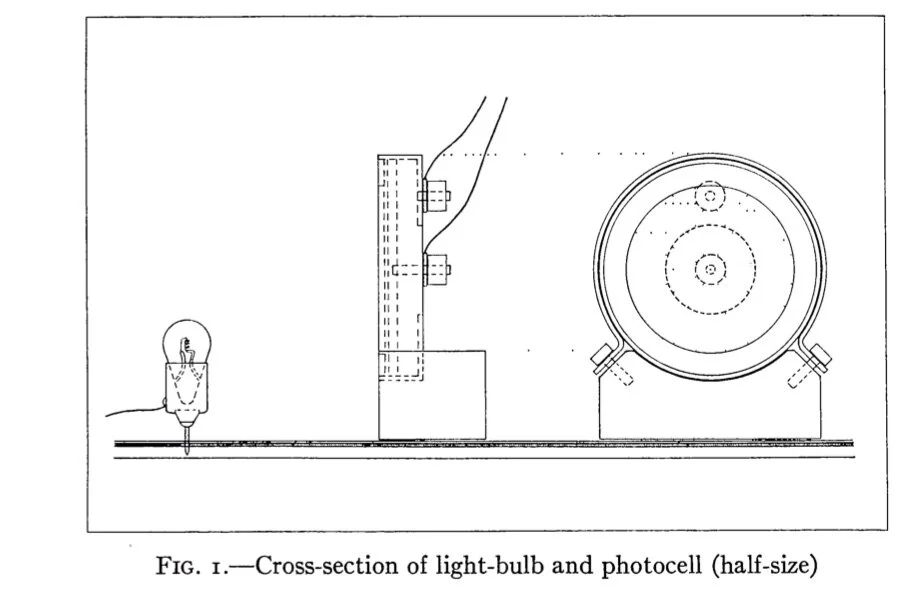
Schematic of the lightbulb and light sensor from Holmberg, E., Astrophysical Journal, vol. 94, p.385
The difficulty with N-body simulations, remember, is that you have to calculate and sum up the forces on each particle from every other particle, and then move that particle in response to that force. But, Holmberg realized, he could skip the first step.
He built a galaxy out of lightbulbs: each lightbulb was a “star” (or really, a single particle representing a huge number of stars). The brightness of each lightbulb represented its mass: the brighter the bulb, the more light it emitted, which was analogous to how much “gravity” the “star” was creating.
Initial conditions of one of the galaxies in th Holmberg Simulation From Holmberg, E., Astrophysical Journal, vol. 94, p.385
To find the force of gravity at a point, Holmberg just had to measure the total intensity of light from his lightbulb-stars at the point — or, since gravity has a magnitude and a direction, he needed to measure the intensity coming from different directions. So, to figure out the force on each star from all the others, he could turn off a single lightbulb-star to prevent it’s own light (that is, its own “gravity” in the analogy), use a lightmeter to measure the directional intensity of the light from all the others, record the “force” that this light would correspond to in the gravitational analogy, and then repeat for every other star. It was tedious and computationally difficult in 1941 (not only no computers, but no general purpose calculators, remember), but it was doable. At least for a small number of stars.
Holmberg wasn’t attempting to simulate a galaxy from initial conditions, like many of the modern $N$-body simulations do. Instead, he was interested in what happened when galaxies collide: how the tidal forces from each galaxy would act to tear them apart.
To do this, he build two “galaxies” as concentric rings of lightbulbs, 37 each (so $N =74$ for the whole simulation), 80 cm in diameter. Much of his paper http://adsabs.harvard.edu/full/1941ApJ....94..385H has to do with concerns that were cutting edge at the time: things like how to ensure a steady electrical supply (and thus predictable light intensity) to his lightbulb-stars, and the use of light sensors to measure the force of “gravity” in his experiment.
He then moved each ring towards each other, with each lightbulb-star being assigned an initial velocity both around the galaxy and toward the other galaxy. Over a span of hours, he would turn off each lightbulb in sequence, find the sum of all the others’ forces on it, and then calculate the resulting acceleration and thus the change in velocity over some simulated time-step. Then, when this was done, each star would be moved forward per its current velocity, and the velocity updated. Then the calculation process would start again. It must have been an huge undertaking, even for an $N$ of “only” 74.
But the results are very cool. He found that the “galaxies” formed tidal tails. as the collision occurred. This is exactly what we see in the Universe today: it is what will happen in the midst of the Milky Way-Andromeda collision. Today, tidal tails are one of those things that, if you take an intro course on astronomy, you’d see when we talk about galaxies. But it’s non-trivial to prove from first principles, and Holmberg showed how they happen. The thing I love the most about this story is it shows how to do science. Holmberg had a question, and he wanted an answer. Today, his problem could be solved in far more detail by the computing power available to anyone with even the simplest smartphone. But he didn’t have that. But he did have some lightbulbs and a lightmeter, and that turned out to be enough.
Tidal tails of two interacting galaxies from Holmberg, E. Astrophysical Journal, vol. 94, p.385
Tidal tails of the Antennae Galaxies (NASA, ESA, The Hubble Heritage Collaboration)