Paper Explainer: Inferring the Morphology of the Galactic Center Excess with Gaussian Processes

This is a paper I wrote with Tracy Slatyer at MIT, her student Yitian Sun (now a postdoc in McGill), Sidd Mishra-Sharma (previously a postdoc at IAIFI, newly hired as a professor at Boston University), and my student Ed Ramirez. I think it is fair to say Ed did the majority of the analysis and coding on this (quite extensive) project, and was instrumental to the project from beginning to end.

This paper is a contribution to a long-running debate within the fields of particle physics and astrophysics, so it is fairly technical in parts, but the debate itself is very interesting and — I think — very important for the field of dark matter.

Dark matter, as you might know, is the material that is postulated to explain a number of “gravitational anomalies” observed in the Universe. Galaxy rotation curves, galaxy clusters, gravitational lensing of clusters, Big Bang Nucleosynthesis, and the Cosmic Microwave Background all point us to a Universe that contains more “matter” than can be accounted for by the census of normal matter built of protons and neutrons. In this context, “matter” has a specific technical definition of “stress-energy that does not have significant relativistic pressure,” which is to say energy that isn’t moving near the speed of light. We call it “dark” because it doesn’t emit, reflect, or interact with electromagnetic waves very much or at all.

At this point, I think dark matter is accepted as the best solution for these gravitationally anomalies. Even models that attempt to solve these issue through modifying gravity pretty much require you to throw in a new particle that doesn’t interact much with regular matter in order to explain all the data. In other words: dark matter.

Theory space of dark matter models, by Tim Tait (2013)

But though dark matter is well-attested gravitationally, we don’t know its particle nature. The number of theoretically motivated models is enormous, and those models probably only scratch the surface on the range of viable models.

To some degree, searching for the particle that makes up dark matter ends up being like the drunk who looks for their keys under the streetlight, because it’s too dark to look elsewhere. Models that provide signals that are testable are more interesting than models that predict that you’ll never see anything. That’s not to say that we don’t want those models to be well-motivated from theory (though perhaps we theorists don’t understand what the Universe considers “well-motivated.” Unfortunately I was not consulted when the nature of dark matter was set, after all).

One of the earliest and best motivated models is dark matter that is produced through interactions with the thermal bath of Standard Model particles early in the history of the Universe. If those interactions are weak enough, and dark matter heavy enough, you “naturally” get the right amount of dark matter at the end of the process. “WIMP” dark matter is one such thermal candidate, though there are many many others.

These models give predictions, and those predictions have been part of our large experimental program to discover the nature of dark matter for many decades now. One of those predictions is that dark matter would still be occasionally interacting and annihilating in space, creating — through those small interactions with the Standard Model — a shower of normal matter that we could in principle see. This shower of particles could include particles (such as pions) that themselves decay to photons, giving gamma rays as a signature, even though dark matter itself does not interact directly with light in this case.

Looking for such signatures of dark matter annihilation is called “indirect detection” and we use gamma ray observatories, most notably the Fermi Gamma Ray Space Telescope, to collect the data that then can be interpreted in terms of dark matter annihilation.

Of course, to look for annihilation of dark matter, you should focus on the regions of the sky where we expect there to be the most dark matter. The best location in that case is the center of our own Milky Way: lots of dark matter, and fairly close by (astrophysically speaking), so the flux of gamma rays from annihilation would be large. Of course, there is the slight problem that the Galactic Center is filled with normal matter, and so the gamma ray flux from there will be combination of many normal “baryonic” sources and then some dark matter, perhaps, on top.

Gamma ray sky as seen by Fermi (Ramirez et al, 2024)

In 2009, Lisa Goodenough (a postdoc at Fermilab) and Dan Hooper (then a staff scientist at Fermilab) looked through the Fermi data at the Galactic Center. Modeling the various backgrounds, they identified a roughly circular “excess” of gamma rays with energies of around 1-2 GeV whose intensity fell off from the center roughly like the expected density of dark matter squared (this is what you expect from a dark matter signal, since annihilation requires two particles to find each other and collide).

If you want to interpret this signal as dark matter, it fits a particle of mass ~50 GeV, annihilating into Standard Model particles (such as $b\bar$ pairs) with the cross section expected of a thermal dark matter relic. It’s a pretty simple model, one I often refer to as the Goodenough Hooperon.

In the years that have followed, many subsequent analyses have confirmed that there is a “Galactic Center Excess” (GCE) with the general properties that Lisa and Dan first identified. Dan in particular has been an advocate for the dark matter interpretation of this signal. It has been searched for in other locations in the sky where significant dark matter annihilation is expected to be seen. In the dwarf galaxies around the Milky Way, we don’t see it, and there’s been lots of papers arguing about this lack of signal. What it comes down to is we don’t have a good enough measure of the dark matter in the centers of these dwarfs to know what the expected signal is, and my feeling right now is that we can’t know for sure. We see a similar signal in the center of Andromeda, but if our own Milky Way GCE isn’t dark matter, we could reasonably expect that the Andromeda signal comes from whatever other baryonic physics is responsible. I did an analysis of the Large and Small Magellanic Clouds gamma ray signal, and we do see something in the LMC consistent with the GCE, but the LMC is too noisy of a gamma ray source to be able to know for sure.

In 2015, Sam Lee, Mariangela Lisanti, Ben Safdi, Tracy Slatyer, and Wei Xue put out an analysis of the GCE that indicated that the signal might be coming from a large number of unresolved point sources in the inner regions of the Galaxy. Point sources are not what we expect the dark matter signal to be, and the proposed mechanism is that the GCE would be gamma rays emitted from the region around millisecond pulsars: rapidly spinning cores of dead stars. These pulsars themselves would be too dim in gamma rays to be seen as a point source, but the analysis suggested that gamma rays were too correlated with each other in spatial origin, and thus we could expect that the GCE was just many many pulsars, all contributing ~10 gamma rays or so to the signal.

This result helped cool interest in the GCE as a signal of new physics — though the possibility never really died. However, outside of people who worked on it, I think the general attitude in the community was that the GCE was a solved problem: it was the result of millisecond pulsars.

In 2019 and 2020, Tracy and Rebecca Leane put out a new analysis that suggested that the point-source hints that were seen earlier were not as statistically robust as originally thought. Mismodeling of the non-GCE components of the gamma ray sky was shown to be capable of being misinterpreted (in simulated tests) as evidence of point sources. This doesn’t mean there aren’t point sources; just that we might need to be less confident in our analysis that said there were.

To some degree this revived interest in the GCE (though not everyone got the memo that the game was back on). At the moment, I think there are two major questions open right now: the first is the question of point sources. The second is the question of the shape of the GCE: its morphology. Separate from the point source debate, multiple analyses have found different shapes and strengths for the GCE. In particular, when we model the gamma ray sky, you can assume a component of gamma rays that trace the stellar bulge in the center of the Galaxy. This bulge looks an awful like the NFW-squared signal we are interested in for dark matter, but not quite. Depending on the analysis, you can find preference for the dark matter-like signal, or — it is claimed — preference for gamma rays coming from a bulge that traces stars. If the latter, that’s less likely to be dark matter.

So, where does our most recent paper fit in?

A year ago, I hosted a small workshop at Rutgers on the status of the Galactic Center Excess. While talking with Tracy and Sidd Mishra-Sharma, we were interested in trying to do an analysis of the shape of the GCE that didn’t require us to know in advance what morphology we needed to assume.

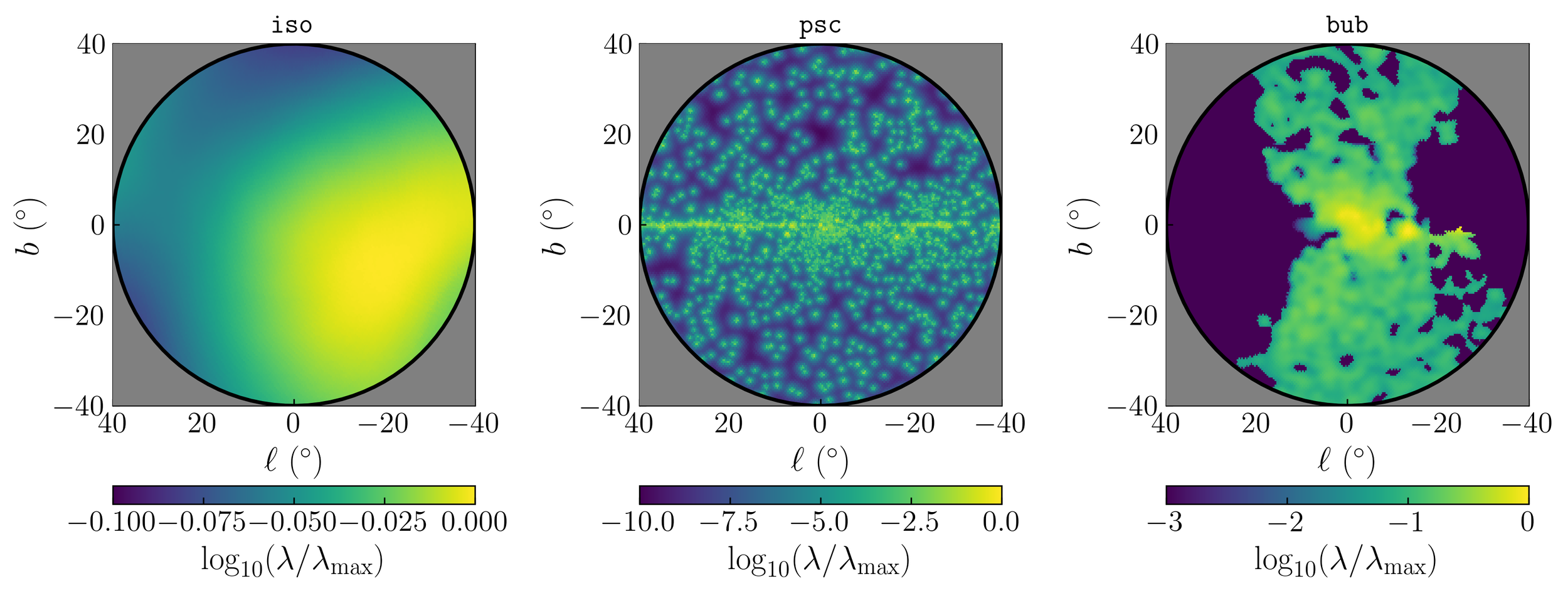
Most of the time, when you do the analysis, you have to pick a shape for your NFW signal and then your bulge template. You also have to pick your templates for your backgrounds. Some of the more popular ones look like the ones shown to the right. The last slide, with six plots, are maps of the NFW dark-matter-like component as well as five of the bulge templates used in the literature.

The differences in the results from different analyses could maybe be traced back to the choice of bulge or other template. Could we instead let the data pick out what the shape of the GCE looked like?

To do this, Sidd suggested we use Gaussian Processes. Gaussian Processes (GPs) are a flexible way of parametrizing a set of data. What they allow you to do is learn from your data a set of functions that the data could plausibly have been drawn from. Unlike neural net-parametrizations, GPs have fewer parameters, and you can place some inductive bias on them to keep them relatively smooth and not overfit data that varies rapidly across different points.

Our thought was to model the GCE with a GP. This allows us to learn the morphology of the data without imposing a specific shape for the bulge and NFW profiles. From the GP, we could then extract statistical preference for various bulge templates, if desired. I asked my student Ed Ramirez to take this on, and he did.

Though GPs are relatively light-weight compared to some machine learning algorithms, there still is a lot of parameters that need to be fit in our data. We want to learn the statistical distribution of the model parameters (the GCE morphology, for example) given the data, and this is a very expensive task given the size of our dataset and the model in question. Fortunately, Sidd and Tracy’s student Yitian Sun had finished constructing a machine learning approach to greatly speed up this computation on Fermi data, using stochastic variational inference. Rather than calculating the quantity we want to learn (the posterior, the distribution of model parameters given the data), SVI calculates a lower bound (the ELBO) using an approximation. Minimizing the ELBO is a good proxy for the task we really want to accomplish.

Inner Region of interest before any point source and disk masking (left), with masking (center), and including outer ROI (right). Ramirez et al 2024

So with all of that out of the way, what did Ed do?

Results of SVI on synthetic data, showing we can recover the true parameters (red) from our analysis chain. Ramirez et al 2024

Well, Ed did a lot of work (seriously, look at the number of appendices in this paper). He took the Fermi data for the GCE and built a center region of interest were we expect the GCE to be present. He modeled the non-bulge backgrounds using known templates, and the GCE itself with a GP, the parameters of which are found using SVI. For this analysis we did not use energy information, adding that will be the next task for a future work. Instead, we used all gamma rays in the 2-20 GeV range. Unfortunately, Ed found that this lack of energy information resulted in a possible fitting issue where some of the backgrounds could absorb the GCE in simulated data. So we had to add a larger ROI at sufficiently large distances from the GC that the GCE isn’t expected to be present. This isn’t ideal, but we expect that the next analysis using energy information will remove this need. Using that set up, Ed showed that we could recover a GCE signal using fake data across a wide variety of mismodeling scenarios.

With all that out of the way, Ed turned to real data. As expected, we find a GCE — everyone finds a GCE, because there’s definitely an excess of gamma rays from the center of the Galaxy. We can pretty rapidly do this analysis for a variety of background assumptions. If fact, we can actually fit to a combination of all possible background templates (80 sets at once), and then extract a GP that represents the GCE given all of those possible backgrounds. It looks like what I show below.

Gaussian Process fit to the Galactic Center Excess with background modeled by linear combination of 80 templates. Ramirez et al (2024)

So we find a GCE. What do we learn about its morphology? That is, after all, the whole reason we did this project. Well, one thing we see is that our “GCE” has a bunch of components that don’t look very Galactic Center-y at all. There’s a bright spot off of the center, and an arm extending off diagonally from the middle. These are likely the result of mismodeling of the other backgrounds, absorbed into the GP because nothing else could take them.

We can fit the GP output to various combinations of dark matter-like NFW profiles and various bulge profiles. Most of the fits prefer the “Coleman2019” bulge shape, but interestingly, the preferred “dark matter” like component is very extended, much flatter across the center of the Galaxy than normally assumed. The center of the GCE is typically fit instead by one of the bulge components.

Preference for various known bulge components when NFW-squared profile is allowed fully flexible model parameters. Ramirez et al (2024).

What’s going on? We think that what we are seeing is that the GP is finding a lot of extended emission that can’t be fit into any of the shapes of the known backgrounds. These backgrounds are maps of gamma rays that are extrapolated from observations in other wavelengths: we see gas and dust in certain places and thus we expect gamma rays. But these templates aren’t perfect, and so it is possible that there’s emission from non-GCE sources that these templates miss. The GP tries to fit them, and in doing so requires a lot of emission far from the Galactic Center. When we fit the GP to our NFW and bulge templates, only the NFW can be modified to absorb the extended emission, leaving the center to be fit by one of the fixed bulge shapes. If we assume a more dark-matter like signal, we also get good fits to the GP (though not as good of course as if we let the NFW morphology float fully)

What this indicates to me is that the morphology one assumes for the stellar bulge and the GCE is really sensitive to the assumptions one makes. By fitting to a GP, making no assumptions of the GCE shape, we still are likely seeing mismodeling of background, but we were able to investigate that in a way that we couldn’t previously. We can’t say for sure what the source of the GCE is from this analysis, but that was never the point. We’ve learned a lot about how our modeling of the GCE can fail, and I’m pretty confident that if we add in energy information (which will likely prevent some of the background-absorption by the GP we saw here), I think we’ll get an even better idea of what the possible morphologies of this signal could be.

All of which is to say: rumors of the Goodenough Hooperon’s demise remain premature, and lots of interesting work remains to figure out what the hell is going on in the center of the Galaxy.